 |
|
 |
|
#include <Geometry.h>
Static Public Member Functions | |
| static double | heightFromEtaBeam (double eta, double b) |
| Altitude, given elevation [rad] and bin distance [m]. | |
| static double | heightFromEtaBeta (double eta, double beta) |
| Altitude, given elevation [rad] and ground angle [rad]. | |
| static double | heightFromEtaGround (double eta, double g) |
| Altitude, given elevation [rad] and ground distance [m]. | |
| static double | betaFromGround (double g) |
| static double | beamFromBetaH (double beta, double h) |
| static double | beamFromEtaH (double eta, double h) |
| The on-beam distance at (elevation) and (altitude). | |
| static double | beamFromEtaBeta (double eta, double beta) |
| The on-beam distance at (elevation) and ground angle (beta). | |
| static double | beamFromEtaGround (float eta, float g) |
| The on-beam distance at (elevation) and ground distance (groundDist). | |
| static double | groundFromEtaBeam (double eta, double beam) |
| Given elevation in radians and on-beam distance, returns the distance from radar to the ground point under the bin. | |
| static double | gammaFromEtaH (double eta, double height) |
Given elevation angle eta and altitude h, returns the ground angle. | |
| static double | groundFromEtaH (double eta, double h) |
| static double | etaFromBetaH (double beta, double h) |
Given ground angle beta and altitude h, returns the elevation angle. | |
| static double | etaFromGH (double g, double h) |
Given ground distance g and altitude h, returns elevation angle. | |
Public Attributes | |
| float | beamWidth |
| std::vector< float > | elevationAngles |
| Note: radians! | |
| std::vector< unsigned int > | bins |
Static Public Attributes | |
| static double | EARTH_RADIUS_43 = 4.0/3.0 * drain::EARTH_RADIUS |
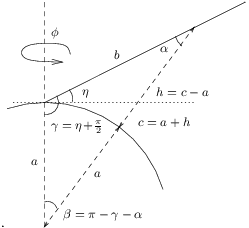
Distances in meters, angles in radians.
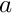
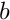
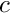
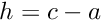
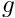
eta 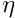
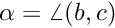

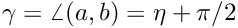
Cosine rule:
![\[
c^2 = a^2 + b^2 - 2ab·\cos(\gamma);
\]](form_176.png)
Sine rule:
![\[
\frac{\sin\alpha}{a} = \frac{\sin\beta}{b} = \frac{\sin\gamma}{c}
\]](form_177.png)
|
static |
The on-beam distance at ground angle beta and altitude h.
By cosine rule:
![\[
b^2 = a^2 + c^2 - 2ac\cos\beta
= a^2 + (a^2 + 2ah+ h^2) - 2a(a + h)\cos\beta
= 2a(a+h) + h^2 - 2a(a + h)\cos\beta
= 2a(a+h)(1-\cos\beta) + h^2
\]](form_171.png)
|
static |
The on-beam distance at (elevation) and ground angle (beta).
By sine rule: sin(beta)/b = sin(alpha)/a => b = sin(beta) * a/sin(alpha).
|
static |
The on-beam distance at (elevation) and ground distance (groundDist).
Let b = beam distance and a = EARTH_RADIUS_. By sine rule: sin(beta)/b = sin(alpha)/a => b = sin(beta) * a/sin(alpha).
Angle(RADAR,BIN)
Angle(BIN->RADAR,BIN->GROUND_POINT)
|
static |
The on-beam distance at (elevation) and (altitude).
By sine rule: sin(gamma)/c = sin(beta)/b => b = sin(beta)*c/sin(gamma).
|
static |
Given ground angle beta and altitude h, returns the elevation angle.
By sine rule:
![\[
\sin(\beta)/b = \sin(\gamma)/c
\Leftrightarrow
\sin(\beta) * c/b = \sin(\gamma)
/// = \sin(\pi-\gamma) =
/// \sin(\pi-(\eta + \pi/2)) = \sin(\pi/2-\eta) = \cos(\eta)
\sin(\pi/2+\eta) = \sin(\pi-(\pi/2+\eta)) = \sin(\pi/2-\eta) = \cos(\eta)
\Rightarrow
\eta = \arccos( \sin(\beta) * c/b ) // WRONG! ALWAYS POSITIVE!
\]](form_173.png)
By cosine rule:
![\[
c^2 = a^2 + b^2 - 2ab\cos\gamma
\Leftrightarrow
\cos\gamma = (a^2 + b^2 - c^2) / 2ab =
= (a^2 + (a^2 + c^2 - 2ac\cos\beta) - c^2) / 2ab
= (2a^2 - 2ac\cos\beta) / 2ab = (a-c\cos\beta) / b
\]](form_174.png)
|
static |
Given elevation angle eta and altitude h, returns the ground angle.
By sine rule:
![\[
\frac{\sin\alpha}{a} = \frac{\sin\gamma}{c} = \frac{\sin\gamma}{a+h}
\Leftrightarrow
\sin\alpha =\frac{a}{a+h}\sin\gamma
\Rightarrow
\gamma = \pi - \gamma - \alpha = \pi - (\eta+\pi/2) - \arcsin \left( \frac{a}{a+h}\sin(\eta+\pi/2) \right)
\]](form_172.png)
|
static |
Altitude, given elevation [rad] and bin distance [m].
The altitude of a point at beam distance (b) and elevation (eta).
By cosine rule:
![\[
c^2 = a^2 + b^2 - 2ab\cos(\gamma);
\]](form_166.png)
|
static |
Altitude, given elevation [rad] and ground angle [rad].
The altitude of a point above ground.
| eta | Elevation in radians |
| beta | Ground angle |
By sine rule:
![\[
\sin(\gamma)/c = \sin(\alpha)/a
\Leftrightarrow c = a · \frac{\sin(\gamma)}{\sin(\alpha)}
\Leftrightarrow h = c-a = a·( \frac{\sin(\gamma)}{\sin(\alpha)} - 1)
\]](form_167.png)
Always
![\[ \sin(\gamma) = \sin(\eta+\pi/2) = \cos(\eta)
\]](form_168.png)
Because 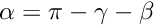
![\[
\sin(\alpha) = \sin(\pi-\gamma-\beta) = \sin(\beta+\gamma)
= \sin(\beta + \eta+\pi/2) = \cos(\beta + \eta)
\]](form_169.png)
Finally,
![\[
h = a·( \frac{\cos(\eta)}{\cos(\beta + \eta)} - 1)
\]](form_170.png)
|
static |
Altitude, given elevation [rad] and ground distance [m].
The altitude of a point at ground distance g and elevation eta.
| eta | Elevation in radians |
| g | Ground distance in metres |
 1.9.8
1.9.8