Loading...
Searching...
No Matches
Public Member Functions | Protected Member Functions | Protected Attributes | List of all members
SegmentStatistics Class Reference

A structure for accumulating coordinates and computing statistics thereof: area, centroid, horizontality, verticality, variance and elongation. More...

#include <SegmentStatisticsProber.h>

Public Member Functions

virtual void clear ()
 Resets the statistics.
 
virtual void add (const int &i, const int &j)
 Accumulate location (i,j) in the statistics.
 
double getSize () const
 Returns the size of the segment.
 
double getMeanX () const
 Returns the horizontal coordinate of centre of mass.
 
double getMeanY () const
 Returns the horizontal coordinate of centre of mass.
 
double getHorizontality () const
 Returns the horizontal variance $\sigma_x$ scaled with total variance $\sigma_x + \sigma_y$. Takes values in [0,1].
 
double getVerticality () const
 Returns the vertical variance scaled with total variance. Takes values in [0,1].
 
double getVariance () const
 Returns the total variance of the pixel coordinates.
 
double getVarianceHorz () const
 
double getVarianceVert () const
 
double getSlimness () const
 Returns the proportion in which the variance equals the variance of an annulus.
 
double getElongation () const
 Returns the proportion in which the variance equals the variance of an annulus.
 
double getEigenValue1 () const
 
double getEigenValue2 () const
 
void toOstr (std::ostream &ostr) const
 

Protected Member Functions

void updateStats () const
 

Protected Attributes

bool _updateNeeded
 
long int size
 Size of segment (area).
 
long sumX
 Sum of coordinates.
 
long sumY
 
long sumXX
 Sum of squared coordinates.
 
long sumYY
 
long sumXY
 
double sizeD
 Size in double precision.
 
double cx
 Center of mass, x coordinate.
 
double cy
 Center of mass, y coordinate.
 
double cxx
 Elements of covariance matrix.
 
double cyy
 
double cxy
 
double eigenValue1
 
double eigenVector1x
 
double eigenVector1y
 
double eigenValue2
 
double eigenVector2x
 
double eigenVector2y
 
double elongation
 

Detailed Description

A structure for accumulating coordinates and computing statistics thereof: area, centroid, horizontality, verticality, variance and elongation.

This class is applied by SegmentStatisticProber which implements the recursive traversal through a segment.

All the statistics are based only on locations (i,j), not on intensities.

Member Function Documentation

◆ getElongation()

double getElongation ( ) const
inline

Returns the proportion in which the variance equals the variance of an annulus.

Returns getSlimness() * (1 - getElongation()). Returns the principal access ratio (e1-e2)/(e1+e2).

Returns
0, if eigenValue1==eigenvalue2, and 1.0 if eigenValue1>>eigenvalue2.

1-e2/e1 = e1-e2 / e1

◆ getHorizontality()

double getHorizontality ( ) const
inline

Returns the horizontal variance $\sigma_x$ scaled with total variance $\sigma_x + \sigma_y$. Takes values in [0,1].

Size [ m_x = \frac{\sqrt{}}{N} ]

◆ getMeanX()

double getMeanX ( ) const
inline

Returns the horizontal coordinate of centre of mass.

Size [ m_x = \frac{1}{N}\sum_{i=1}^N x_i ]

◆ getMeanY()

double getMeanY ( ) const
inline

Returns the horizontal coordinate of centre of mass.

Size [ m_x = \frac{1}{N}\sum_{i=1}^N x_i ]

◆ getSize()

double getSize ( ) const
inline

Returns the size of the segment.

Size [ s = ]

◆ getSlimness()

double getSlimness ( ) const
inline

Returns the proportion in which the variance equals the variance of an annulus.

The variance returned by getVariance() is defined as

\[ E\left[ (x-x_m)^2 + (y-y_m)^2 \right] = E\left[ r^2 \right] \]

where $r$ is the distance from centroid $(x_m,y_m)$.

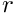
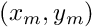
For an annulus, with inner radius 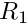$R_1$ and outer radius $R_2$, the area is

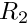
\[ A = \int_{R_1}^{R_2} \int_{0}^{2\pi} r d\alpha\! dr = \pi (R_2^2 - R_1^2) \]

and the variance

\[ E\left[ r^2 \right] = \frac{1}{A} \int_{R_1}^{R_2} \int_{0}^{2\pi} r^2 r d\alpha\! dr = \frac{2\pi}{A}\int_{R_1}^{R_2} r^3 dr = \frac{2\pi}{4\pi (R_2^2 - R_1^2)} (R_2^4 - R_1^4) = \frac{R_2^2 + R_1^2}{2} \]

Hence, for circular areas the variance varies between 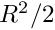$R^2/2$ (for circle) and $R^2$ (for infinitesimally thin annulus). Obviously, these are the lower and upper limits of variance also for segments of any shape (consider a set of points, starting from two).

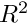
However, thin line segments achieve values close to those of annula. Consider a thing rectangle of "radius" 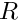$R$, ie height $2R$:

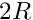
\[ E\left[ (x-x_m)^2 + (y-y_m)^2 \right] \approx E\left[ (y-y_m)^2 \right] = \int_{-R}^{R}y^2dy/\int_{-R}^{R} dy = \frac{1}{3}\frac{R^2+R^2}{R+R} = \frac{1}{3}R^2 \]

(Under construction.)

If a segment is circular, its radius squared is 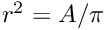$r^2=A/\pi$, where $A$ is the area returned by getSize(). Hence, given a segment of size $A$ the variance lies between $A/2\pi$ and $A/\pi$. The annularity is the variance normalized to these limits:

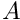
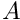
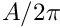
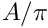
\[ \mathrm{annularity} = \frac{\sigma^2-A/2\pi}{A/\pi-A/2\pi} = 2\pi\sigma^2/A - 1. \]

◆ getVariance()

double getVariance ( ) const
inline

Returns the total variance of the pixel coordinates.

Returns the squared mean radius from the centroid. In physics, moment of inertia corresponds to this quantity, assuming that the body has constant density.

◆ updateStats()

void updateStats ( ) const
inlineprotected

Near undetectValue

The documentation for this class was generated from the following file:
Generated by   doxygen 1.9.8